
www.rit.edu/asc Page 1 of 9
1. Area under a curve – region bounded by the given function, vertical lines
and the x –axis.
2. Area under a curve – region bounded by the given function, horizontal
lines and the y –axis.
3. Area between curves defined by two given functions.
1. Area under a curve – region bounded by the given function, vertical
lines and the x –axis.
If f(x) is a continuous and nonnegative function of x on the closed interval [a, b], then the
area of the region bounded by the graph of f, the x-axis and the vertical lines x=a and x=b
is given by:
b
a
dxxfArea )(
When calculating the area under a curve f(x), follow the steps below:
1. Sketch the area.
2. Determine the boundaries a and b,
3. Set up the definite integral,
4. Integrate.
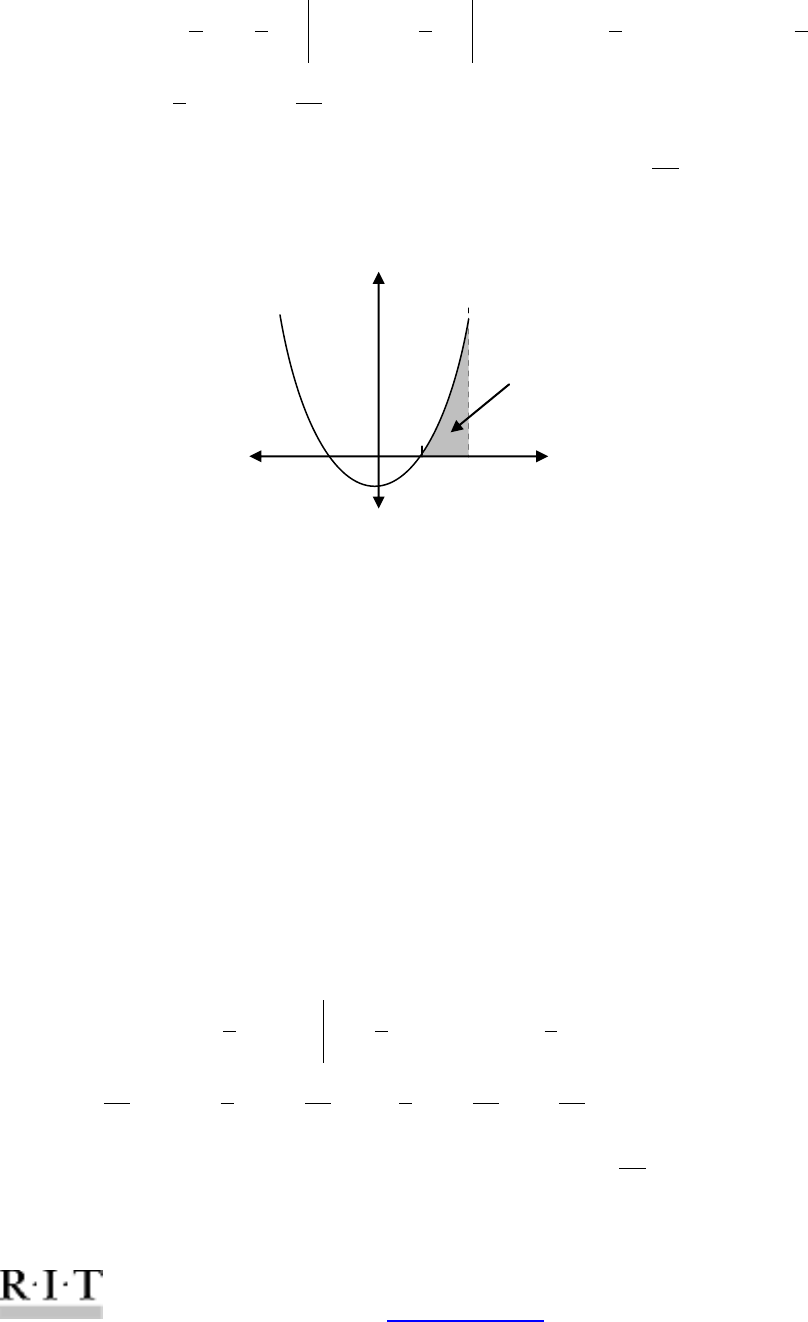
Ex. 1. Find the area in the first quadrant bounded by
2
4)( xxxf
and the x-axis.
Graph:
To find the boundaries, determine the x-intercepts:
040)(
2
xxxf
0)4( xx
0x
or
0)4( x
so
0x
and
4x
Therefore the boundaries are
0a
and
4b
Areas by Integration
A
www.rit.edu/asc Page 2 of 9
Set up the integral:
4
0
2
)4()( dxxxdxxfA
b
a
Solve:
3232
4
0
32
4
0
32
4
0
2
0
3
1
024
3
1
42
3
1
2
3
1
2
1
4)4( xxxxdxxx
3
32
064
3
1
162
The area in the first quadrant under the curve
2
4)( xxxf
is equal to
3
32
square units
Ex. 2. Find the area bounded by the following curves:
,4
2
xy
,0y
,4x
Graph:
Finding the boundaries:
,4
2
xy
and
0y
implies
04
2
x
so
022 xx
2x
or
2x
From the graph we see that
2x
is our boundary at a. The value
2x
is a solution to the
equation above but it is not bounding the area. (Here’s why the graph is an important tool to help
us determine correct results. Don’t skip this step!)
The other boundary value is given by the equation of the vertical line
,4x
Boundaries are:
,2a
and
,4b
Set up the integral:
4
2
2
)4()( dxxdxxfA
b
a
Solve:
242
3
1
444
3
1
4
3
1
)4(
33
4
2
3
4
2
2
xxdxx
3
32
8
3
56
8
3
8
16
3
64
8
3
8
16
3
64
The area bounded by the curves
,4
2
xy
,0y
,4x
is equal to
3
32
square units.
b
a
A
www.rit.edu/asc Page 3 of 9
2. Area under a curve –given function, region bounded by the horizontal lines
and the y –axis.
In certain problems it is easier to rewrite the function in terms of y and calculate the area using
horizontal elements. In this case the formula for the area would be:
d
c
dyygArea
When calculating the area under a curve, or in this case to the left of the curve g(y), follow
the steps below:
1. Sketch the area.
2. Determine the boundaries c and d,
3. Set up the definite integral,
4. Integrate.
Ex. 3. Find the first quadrant area bounded by the following curves:
2
2
xy
,
4y
and
0x
.
There are two ways to solve this problem: we can calculate the area between two functions
4y
and
2
2
xy
using the vertical elements and integrate with respect to x, or we can use the
horizontal elements and calculate the area between the y-axis and the function
2
2
xy
integrating the functions with respect to y.
We will solve it using the second approach by considering horizontal elements and the function in
terms of y.
The formula we will use is:
d
c
dyygArea
, so we need to determine the boundary values
c and d first.
The boundary value d corresponds to the horizontal line
4y
. To calculate c, we need to locate
the y-intercepts. Therefore set
0x
and solve the equation
2
2
xy
for y; hence
2y
. So the
boundaries are
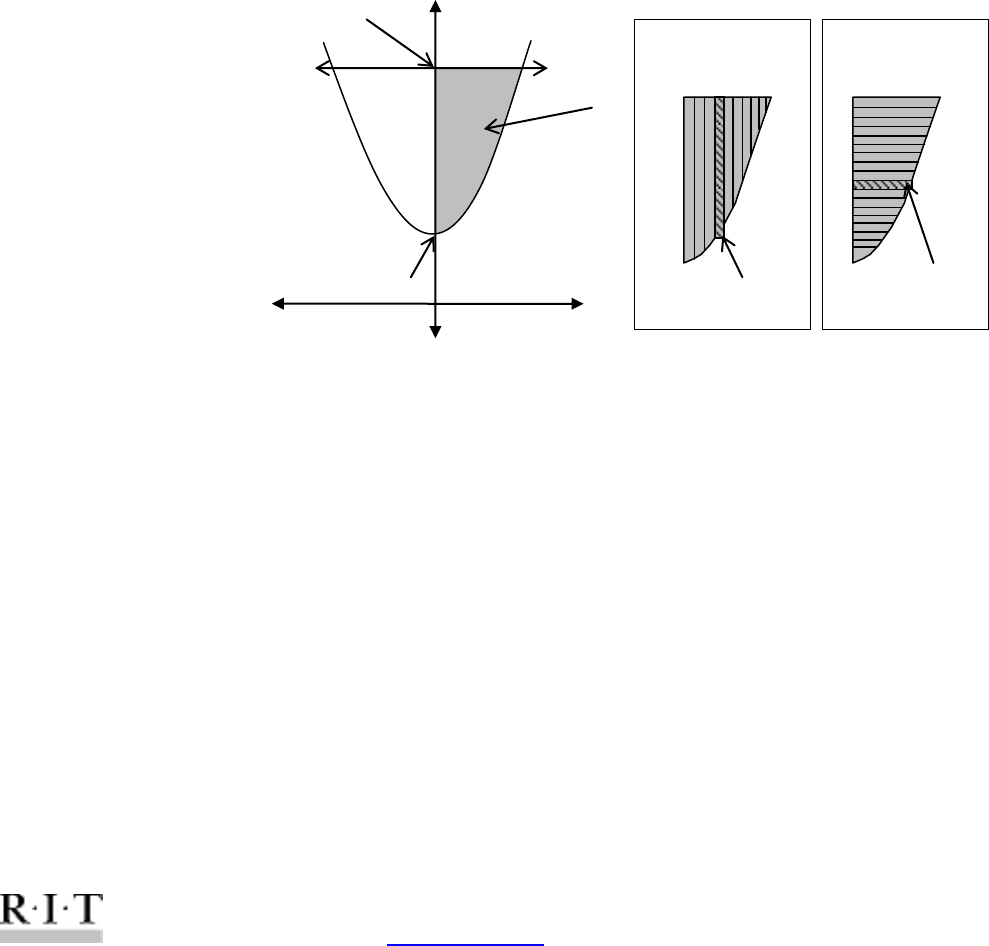
“vertical
elements”
d
c
A
Typical rectangle
(with width of dx)
“horizontal
elements”
Typical rectangle
(with width of dy)
www.rit.edu/asc Page 4 of 9
Now we need to find our g(y). That is easily done by solving
2
2
xy
for x.
2
2
2
2
2
yx
yx
xy
We will ignore the negative radical, since our area is in the first quadrant.
Now let’s set up the integral:
dyyA
4
2
2
Solve the integral using a simple u substitution:
3
24
02
3
2
22
3
2
24
3
2
2
3
2
2
333
4
2
3
4
2
ydyyA
square
units.
The first quadrant area bounded by the following curves:
2
2
xy
,
4y
and
0x
is equal to
3
24
square units.
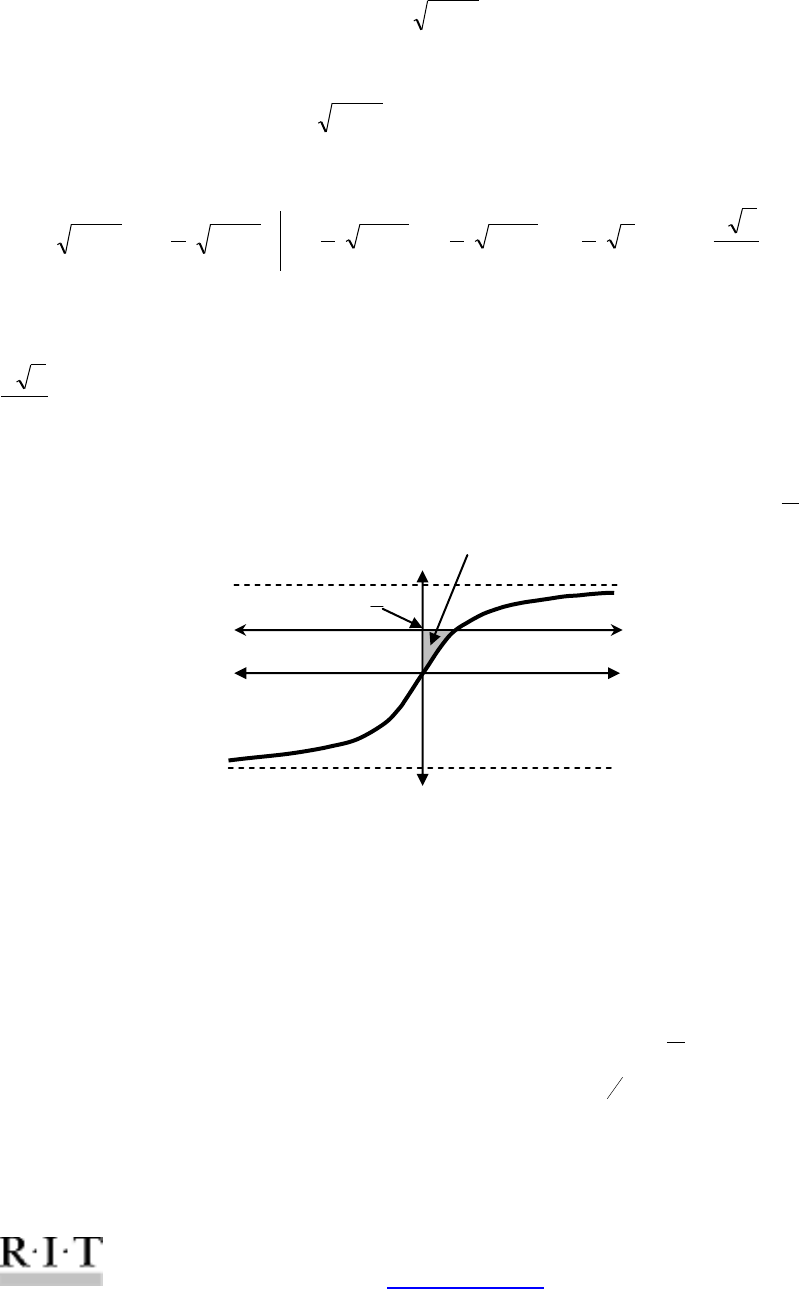
Ex. 4. Find the first quadrant area bounded by the following curves:
xy arctan
,
4
y
and
0x
.
Since it is much easier to integrate
yx tan
than
xy arctan
, we will rewrite the given
function in terms of y, and integrate using the horizontal elements and the formula:
d
c
dyygA
to find the area. The function
xy arctan
implies
yx tan
. So
yyg tan
.
The lower boundary c=0 is easily obtained from the graph or by solving the equation
0arctan x
. The upper boundary is given by the equation of the line:
4
y
.
So the area we are looking for is given by the following integral:
4
0
tan
ydyA
A
4
x
y
www.rit.edu/asc Page 5 of 9
Solving the integral yields:
2ln
2
1
2ln
2
1
2ln02ln2ln
1ln
2
2
ln0cosln
4
coslncoslntan
4
0
4
0
yydy
So the first quadrant area bounded by the following curves:
xy arctan
,
4
y
and
0x
is
equal to
2ln
2
1
square units.
3. Area between two curves.
This can be considered as a more general approach to finding areas. Thus each of the previous
examples could have been solved using such an approach by considering the x- and y- axes as
functions with equations y=0 and x=0, respectively.
Many areas can be viewed as being bounded by two or more curves. When area is enclosed by just
two curves, it can be calculated using vertical elements by subtracting the lower function from the
upper function and evaluating the integral.
Analogously, to calculate the area between two curves using horizontal elements, subtract the left
function from the right function.
As always, a sketch of the graph can be a very important tool in determining the precise set-up of
the integral. If you subtract in the wrong order, your result will be negative. That mistake can be
avoided by taking the absolute value of the difference of the functions.
Here is the universal formula for finding the area between two curves:
Using the vertical elements:
b
a
dxyyArea
12
where y
1
and y
2
are functions of x
Using the horizontal elements:
dyxxArea
d
c
12
where x
1
and x
2
are functions of y.
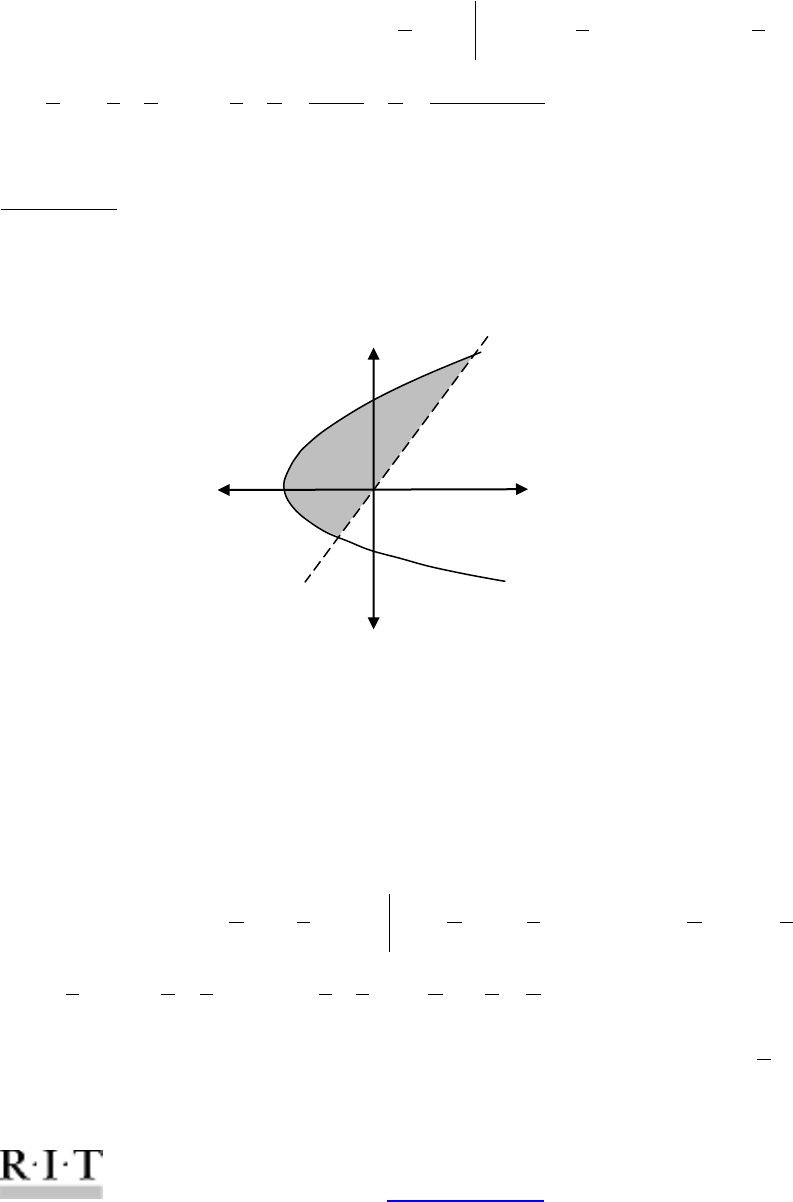
Ex.5. Find the area of the region enclosed by the following curves:
x
ey
1
,
1
2
2
xy
,
1x
and
1x
.
As always, we will first draw a sketch.
1
2
xy
x
ey
1x
1x
www.rit.edu/asc Page 6 of 9
In this case it is fairly easy to integrate the functions as given with respect to x. So the boundaries
are:
1a
and
1b
.
Notice that in the region that we are interested in, the function
x
ey
1
is above the function
1
2
2
xy
, thus the integral set up should look as follows:
1
1
2
1 dxxeA
x
Solving it:
11
3
1
11
3
1
3
1
11
3
1
3
1
1
1
3
1
1
2
1
1
2
eexxedxxedxxe
xxx
e
ee
e
e
e
e
e
e
3
343
3
41
3
41
3
21
3
2
22
.
So the area of the region bounded by
x
ey
1
,
1
2
2
xy
,
1x
and
1x
is equal to
e
ee
3
343
2
square units.
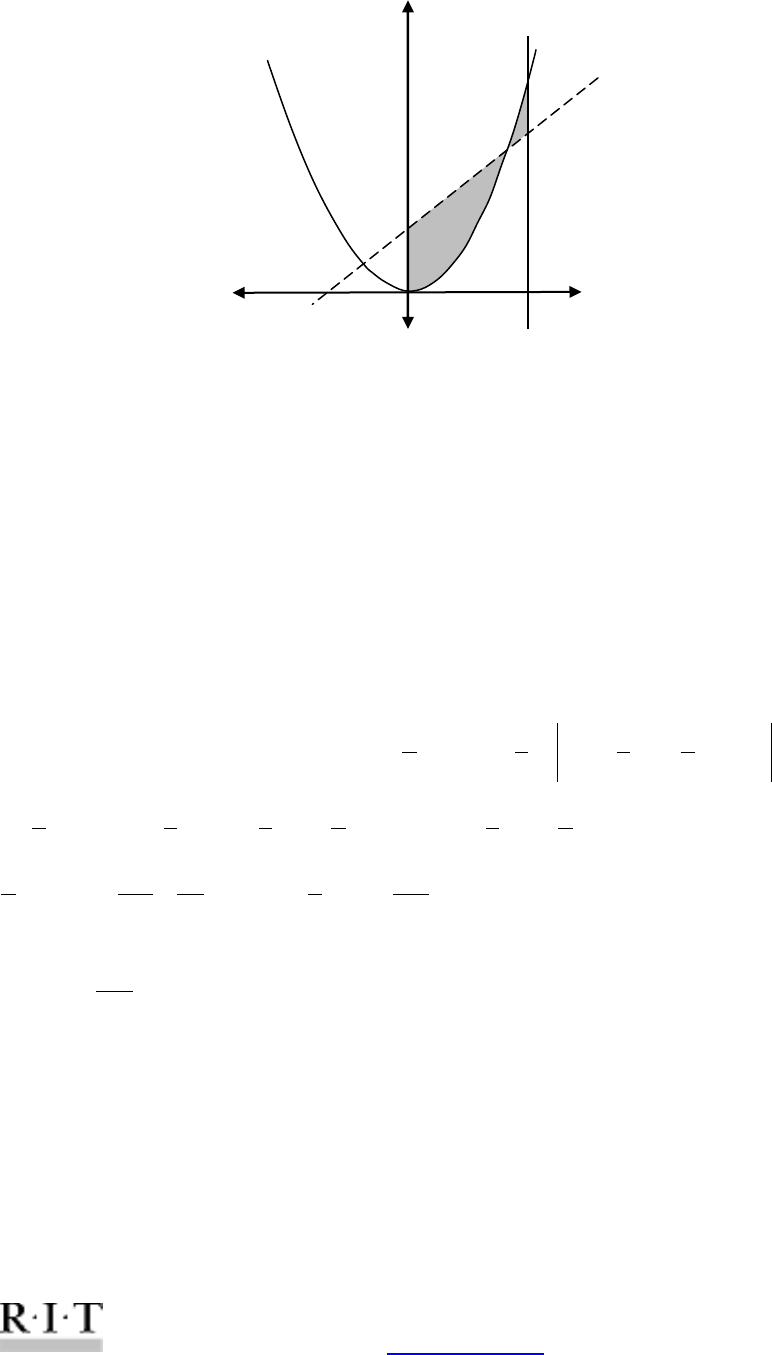
Ex.6. Find the area of the region enclosed by the following curves:
2
2
1
yx
, and
yx
2
.
Since the first function is better defined as a function of y, we will calculate the integral with
respect to y.
As usual – draw the picture first:
In this case the boundaries are determined by the points of intersection of both functions.
Remember that we want the y-values since we will be integrating with respect to y.
We need
21
xx
. This implies
yy 2
2
and
02
2
yy
12 yy
2y
or
1y
So
1c
and
2d
. The “left” function is
2
2
1
yx
and the “right” function is
yx
2
.
121
3
1
1
2
1
222
3
1
2
2
1
2
3
1
2
1
2
3232
2
1
2
1
322
yyydyyyA
2
9
2
1
4
2
1
2
3
1
3
8
62
3
1
2
1
4
3
8
2
square units.
So the area of the region enclosed by the curves:
2
2
1
yx
, and
yx
2
is equal to
2
9
square
units.
2
2
yx
xy
www.rit.edu/asc Page 7 of 9
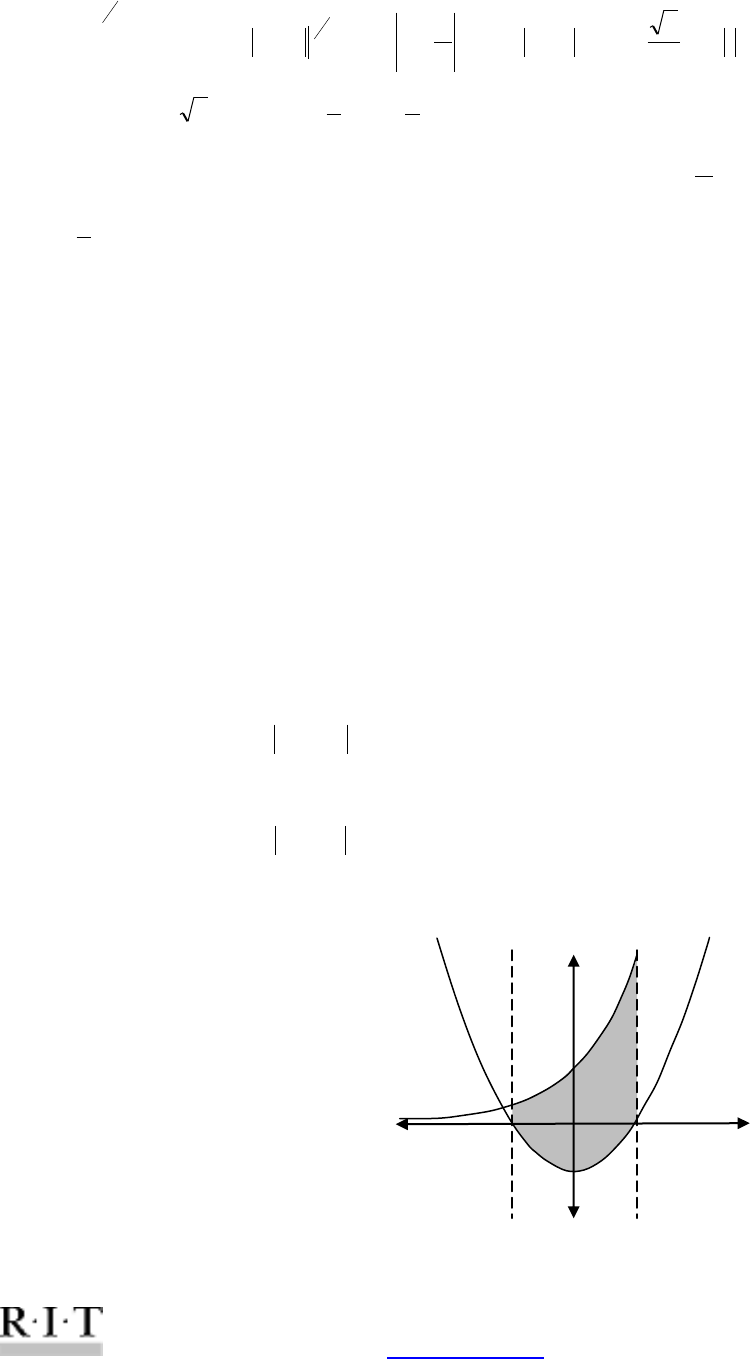
Ex.7. Find the area of the region enclosed by the following curves:
2
xy
,
6 xy
,
0x
and
5x
As usual – sketch a rough graph first:
In this case it is very important to draw the graph, since the functions intersect between the
boundaries. This means that we will have to actually calculate two separate integrals and then add
the results. Otherwise we would end up subtracting the two pieces from each other.
First we need the “middle” intersection point so we will solve the equation:
5
2
xx
05
2
xx
023 xx
3x
or
2x
The intersection point at
2x
is outside our area. We are interested in
3x
, this is our
“middle” boundary value.
In this case the integral set-up will look as follows:
5
3
23
3
0
32
3
0
5
3
22
6
2
1
3
1
3
1
6
2
1
66 xxxxxxdxxxdxxxA
363
2
1
3
3
1
565
2
1
5
3
1
3
3
1
363
2
1
232332
6
157
18
2
9
930
2
25
3
125
918
2
9
square units.
So the area of the region enclosed by the curves: :
2
xy
,
6 xy
,
0x
and
5x
is equal to
6
157
square units.
2
xy
6 xy
5x
0x


